舶用エンジンの主機の設計に携わっていると、エンジン回転数と出力が3乗に比例すると教わることがあると思います。あまりにも一般的すぎて、その理由まできちんと説明されることが少ないと思いますので、今回、わかりやすく解説します。
船速とプロペラ回転数の関係
まず、船舶はプロペラによって推進され、前に進んでいますので、船速とプロペラの関係について説明します。
プロペラは設計概念がネジと似ていまして、「ピッチ」が定義されています。「ピッチ」とは、プロペラが一回転したときに、進む距離のことです。
プロペラが1回転することによって進む距離が決まっているので、時間の項をそれぞれに加えると、プロペラ回転数(1分間当たりに回転する数)と船速は比例の関係にあることがわかります。
ピッチ = 距離(m) / プロペラ1回転
船速V (km/h) ∝ プロペラ回転数N (min-1)
プロペラの回転数が速くなればなるほど、それに比例して、船速も速くなるという事を表しています。
船舶の抵抗と船速の関係
次に、船舶が水上を推進する時の水の抵抗について考えます。この抵抗は、流体抵抗と同じように考えることができ、船速の2乗に比例します。
詳しくは流体力学で習うので、割愛しますが、以下のような関係式になります。
抵抗力F ∝ 1/2 x 船速V^2
船速が速くなればなるほど、その2乗に比例して、抵抗力が増加する(船が前に進みにくくなる)という事を表しています。
エンジントルクと抵抗の関係
ここでやっと、エンジンが出てきます。エンジントルクが船舶の抵抗力と同じだけの力を出して、等しい速度を保てるようになりますので、そのまま比例の関係になります。
トルクT ∝ 抵抗力F
エンジンは、船の抵抗力と比例の関係でトルクを出す必要があるという事を表しています。
抵抗力と同じトルクであれば同じ速度をキープして、もし加速したければ、より大きいトルクを出して抵抗力に打ち勝つ必要があるという事ですね。
エンジン出力とトルクの関係
エンジン出力とトルクの関係は過去の記事で説明しましたので、詳細は割愛しますが、以下の関係式になります。
出力P = 2 x π x トルクT x 回転数N / 60
エンジン出力と船速の関係に整理
ここまでの関係式を基に整理し直すと、以下のようになります。
トルクTは抵抗Fに比例し、抵抗Fは船速Vの2乗に比例し、船速Vは回転数Nに比例するため、トルクTは回転数Nの2乗に比例します。
エンジン出力PはトルクTと回転数Nの掛け算に比例しますので、エンジン出力Pは回転数Nの3乗に比例します。
エンジン出力P ∝ 船速回転数N^3
回転数と船速は比例の関係でしたので、つまり、
エンジン出力P ∝ 船速V^3
となります。やっと上記の関係式に辿り着きました。
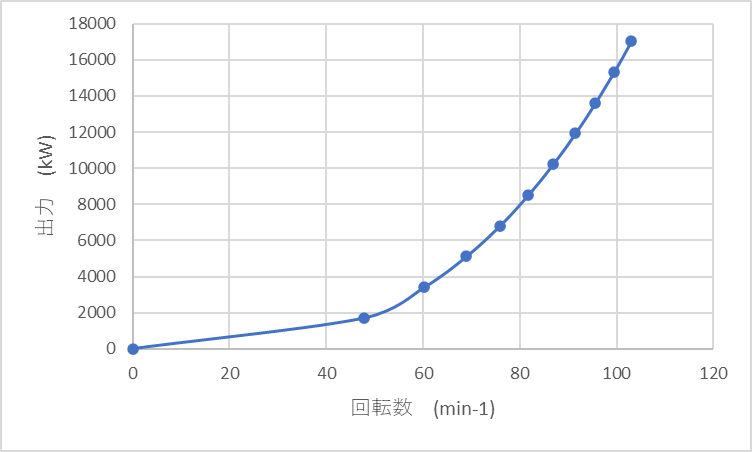
参考として、MANの7G60ME-C10.5の出力と回転数をプロットしてみました。以下のグラフのように、出力は3乗に比例したカーブになります。回転数(船速)を上げれば上げるほど、出力をどんどん出さないといけなくなるというイメージができるかと思います。例えば、50から100へ2倍の回転数(船速)を出そうとすると、約2000から約16000へ8倍(2の3乗で8倍)の出力が必要になっていることがわかるかと思います。すごい増え方ですね。このような理由から、船はゆっくり走る方が燃料を節約できる事がわかりますね。
まとめ
丁寧に説明しましたので、長くなりましたが、抵抗は2乗に比例する、出力は3乗に比例すると覚えて頂ければ良いと思います。工学の世界でもよく「2乗3乗の法則」が出てくることがありますので、その良い一例ですね。









コメント